My experiments with Mathematics

Maths from my childhood:

The moment we hear the word Maths, we think of calculations and formulae. For some, Maths is easy and for others, it is a hard nut to crack. For me, Maths has been a fascination. To me, Maths means – the ability to understand the universe with numbers, representation of the physical universe in a simple equation, reducing a complex structure to its fundamental geometrical representation.

As a student, I was pretty good at scoring marks in Maths, which did not necessarily mean I was conceptually good. Most of my Maths skills were memory-based and this memory assisted me in keeping up good grades. As I grew fond of Physics in my Grade 12 and later part of academic life, Maths started to attract me more. Today I coach students on how to learn Maths in simple ways at NumberNagar®.

December is the month I don’t like for its chilly weather, but I love it for clear skies and S Ramanujan’s birthday. S Ramanujan is usually introduced as a child prodigy in Maths to inspire us in school. But we don’t ever get to study his work in 17 years of school and college life. To keep up the spirit of the season, I am sharing with you a few experiments in Maths that I loved growing up with.

Experiments with Maths:

#1 – The constant ratio:

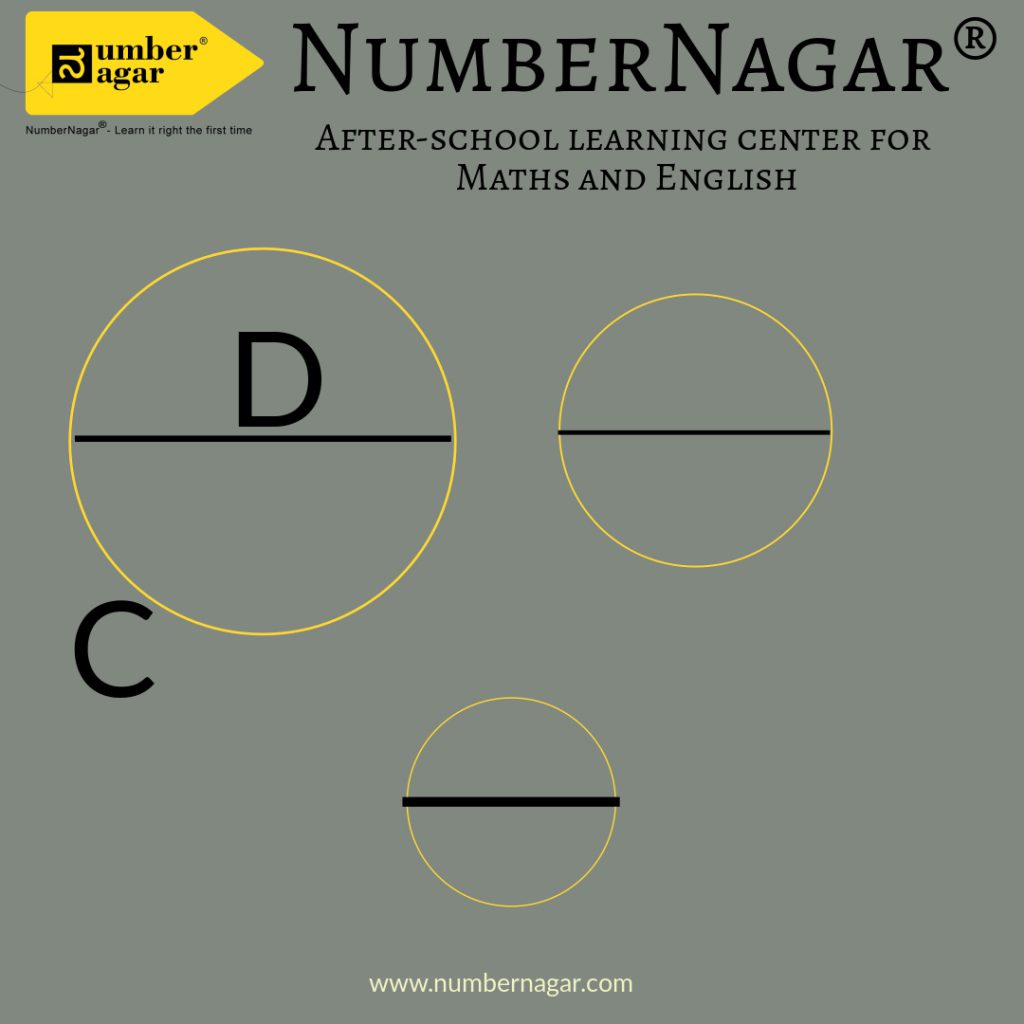
Historical data suggests that circle as a geometric figure has intrigued some of the greatest minds. It was seventh grade and in the class of CAS ma’am, we were drawing circles. The next thing I noticed was that there were 6 circles of different radii, small to big, drawn on the board. Then we were asked to measure the diameter (the straight line joining two opposite points in a circle going through the centre). Like good experimenters, we tabulated the data of circumference of the circle and its corresponding diameter. So far it was just a mechanical job. What came next was the fascinating part. We then were asked to calculate the ratio of the circumference (C) to diameter (D). It was so fascinating to observe that the ratio was always a constant no matter what the values of C and D were (refer figure 1).

I do this every time I teach circles. You too can try it with circular bottle caps or plates at home.

#2 – The LCM:

I should tread carefully on this topic as most of my students hate it from the bottom of their hearts. I have come to understand that their difficulty in finding LCM has its roots in the lack of memory of multiplication tables.

In the era I grew up, the OHP – Over Head Projector was the ultimate technology that made presentations attractive and mind-blowing. The connection to this experiment is the OHP sheet. Earlier, the content on OHP sheet was hand-written. Later when colour printers became easily accessible, OHP sheets became more colourful and well organised (in my case).

I have used this OHP sheet for experiments with LCM. We call it the LCM toy at NumberNagar®. The toy has 10 x 10 boxes in which the boxes are shaded according to the multiplication table in hand. (Refer figure 2).

This is how the toy is used:

• Place the 10 x 10 grid of numbers (1 to 100) on the bottom
• Place the shaded sheet of any number (Eg: 4) on top of the number grid – this will now show only the multiples of 4
• On top of this, place the shaded sheet of another number (Eg: 9) – the first number that is visible from top left is the LCM of these two numbers – 4 and 9

This is a very simple tool but gives a long-lasting understanding of LCM. I train all my students to create this toy on their own using any transparent sheet. All they need to do is create a 10 x 10 grid of numbers and then the shaded sheets for multiples of 2 to 10. This helps them understand the method of finding LCM. You can try this too.

#3 – Geometry of the algebraic identity (a + b)³

How many terms does this expression have? As there are two variables, this expression will have 2³ = 8 terms. In the expanded form, it is a³ + b³ + 3a²b + 3b²a. We all know this out of memory and have used this formula numerous times in school while solving problems.

Now, what does this equation represent physically? This represents a cube that is made up of 2 smaller cubes and 6 cuboids. Watch video 1 below, every piece of the puzzle is a term in the above equation. Putting the pieces together to form a big cube generates a visualisation of the algebraic expression (a + b)³. I generally ask students to build these cubes using origami methods and then assemble them to visualise and understand the meaning of (a + b)³.

The next step is to extend this understanding to (a + b + c)³. Here the expression will have 3³ = 27 terms. Similarly, a combination of 3 cubes and 24 cuboids forms the bigger cube. Once students get a hang of this, I ask them to try (a – b)³. At this juncture, most of them give it a shot but give up after a couple of trials. Now, why don’t you try to explore this?

#4 – Squares and rectangles:

Try this out: Take an A4 sheet of paper and cut a square out of it by folding the right-hand top corner to touch the opposite side symmetrically. Tear off the rectangular sheet that is left at the bottom (remember how you made a boat when you were kids, this is the first step)

With the square piece of paper make a rectangular fold from the right side for 5 cm. Repeat the same from the top edge. Now, you have a smaller square at the right-hand top corner and a large square at the left-hand bottom corner. There are also two rectangles – one on the left-hand top and the other on the right-hand bottom corner.

If you have followed the instructions clearly, you will see the pattern 6 shown in figure 3 below. Also, watch video 2 below to get quick instructions on creating this yourself. Now, guess the algebraic identity that you are holding in your hand.

Yes you are right! It is the famous (a + b)².

Now, if we cut each of these pieces apart and rearrange them, do you see a pattern? Look closely at figure 4. Do you see the connection? Before sculpting any idol, artists usually use proportions and layout. Now you know what the artist might have used before carving the statue of Buddha.

Explore the beauty of Maths yourself:

There are over 600 such activities that you can engage yourself and your loved ones at NumberNagar®. All you need to do is visit your nearest centre and get a meaningful learning experience.

Happy winter and a mathematical season to you all!

The following two tabs change content below.

• Bio
• Latest Posts

Sriraghavan S M

Sriraghavan (Raghu) is an Astronomer by qualification (MSc, Astronomy, Bangalore University) and a teacher by passion. He is a trained counsellor and psychotherapist. His firm belief and conviction to transform the education system in India led him to be an entrepreneur through NumberNagar®. His core work at NumberNagar® revolves around product presentations, academic content, and training. He teaches Maths and Science to young students, rubbing off his passion to them. He trains teachers as well, inspiring them to better themselves. He has taught Physics in educational institutes, during his early career days. He has travelled extensively all over Karnataka, training teachers and popularising Astronomy. He advocates multiple intelligence and is constantly on the lookout for new things to learn. He is ambidextrous and enjoys sketching. He was an avid cricket player in his younger days. He is an enthusiastic biker and uses long solo motorcycle rides as means of reflection and rejuvenation.

Latest posts by Sriraghavan S M (see all)

• Why self-directed learning is the need of the hour - 2 July 2021
• Discovering my teaching method - 8 January 2021
• Finding Balance - 23 October 2020
• A case for Alternative Learning - 9 October 2020
• Why I am a teacher - 4 September 2020