An ongoing quest
Being a Software Architect and a UX (User Experience) person, I have a different perspective of looking at the physical things. When I look around while I’m driving, walking or just doing many other things, I find very interesting mathematical shapes. Some of these are very simple while others are complex. Some anyone can see, while others can be seen only by the trained eyes.
You may argue how someone accustomed to working with virtual things (e.g., code, design, architecture) can have an eye for physical things? My response to that is, you just need to have the willingness to look and discover and these mathematical shapes are all there. They are like waiting to be discovered by us. You don’t have to go to a museum or to an architectural marvel to discover them.
Finding mathematical shapes around you
Let’s look at some of the mathematical shapes we can find around us. You will be surprised to see what you find and how important they are to us.
Geometrical shapes in buildings facades
Next time when you are in front of a building, look at the “facade” of the building. Facade is a French term which means the external side of the building, especially the front?
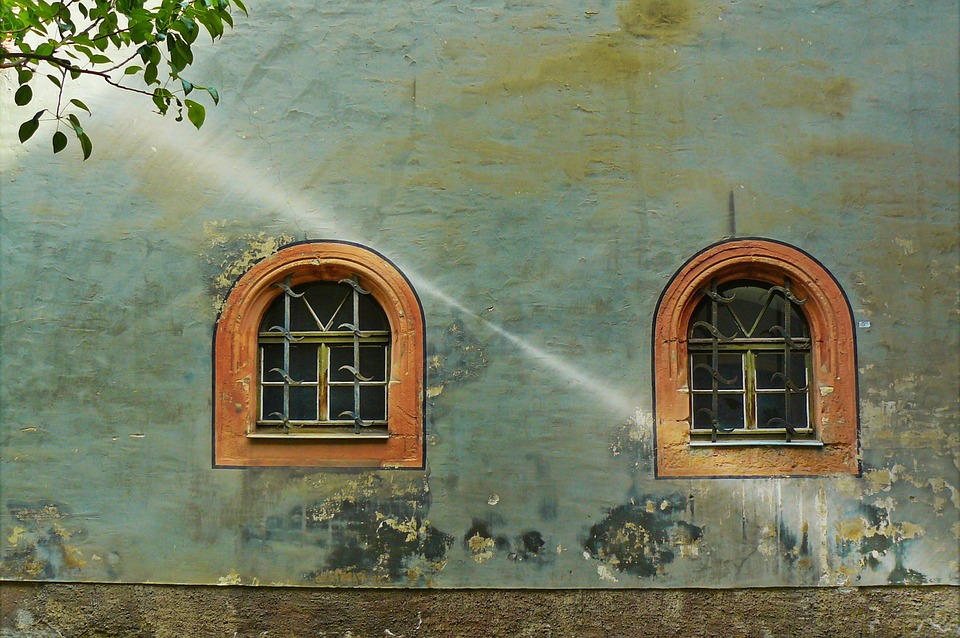
Image Credit: Pixabay / cocoparisienne
What do you see? Do you see any geometrical shapes? If you look closely, you will see many geometrical shapes, circles, rectangles, squares, arcs, and many other combination shapes.
These shapes are important for aesthetics and architectural stability of the building. They play a major role in keeping the structure intact for generations to come. These geometrical figures are the main reason behind the structural integrity of these man-made artifacts.
You can do this quick experiment no matter where you are, be it an apartment complex, a religious structure, or a government building. You are bound to see many geometrical shapes.

Image Credit: Pixabay / Tama66
Mathematics behind bridges
Every bridge you might have seen can tell a different story. The geometrical shapes which support a bridge are always an engineering marvel.

Did you know? There are 5 different types of bridges – Beam bridges, Arch bridges, Cantilever bridges, Cable-stayed bridges, and Suspension bridges.
Read more about them at WikiPedia article about Bridge.

Bridges serve one basic purpose of connecting two points that are otherwise disconnected and difficult to access. Generally, it provides the shortest distance between the two points. The art and science of constructing these structures rely heavily on mathematics and consequently the physics of stress and load.
Some of the prevailing factors that influence the designs and types of structures include the intended use and users, the available constructing materials, environmental conditions, cost, adequate manpower, the length of the span, the type of river banks, present and projected traffic load, the free height under the bridge, aesthetic considerations and the available technology.
Reference: The Basic Mathematics of Bridges

So you see now that these are intricate structures with mathematics in their core.
Mathematics in nature – Life revolves around Fractals
Fractals are self-repeating geometrical shapes. They can also be visualised as never-ending patterns. This means if you take a small part of a fractal it will resemble the whole. You can continue going smaller and smaller and yet this property will never cease to exist.
Fractals permeate our lives, appearing in places as tiny as the membrane of a cell and as majestic as the solar system. Fractals are the unique, irregular patterns left behind by the unpredictable movements of the chaotic world at work.
Fractals have intricate mathematics associated with them. The same mathematics can be used to create very complex self-repeating shapes which are used extensively in graphics and game development.

Image credits: Pixabay/Wow Phochiangrak
Fractals have always been associated with the term chaos. We can elegantly describe fractals as “the patterns of chaos.” Fractals depict chaotic behaviour, yet if one looks closely enough, it is always possible to spot glimpses of self-similarity within a fractal.

Image credits: Pixabay/Gerd Altmann
Where else in your surroundings can you see mathematics in action?
I’ve given only a few examples of where to find mathematical shapes around you. If you keep looking, you’ll find it everywhere. The whole world is a playground if you are looking to learn Mathematics in a fun and curious way.
Some other examples are:
- Household – Try to find mathematical shapes and applications in household appliances and utensils
- While traveling – Next time when you are traveling inside your city or outside of it, see if you can find mathematical shapes in the locomotion of your choice, e.g., in trains, buses, airplanes, and so on.
- While in the grocery store – See how balance works, how the fresh vegetables are stacked, and many other such examples.
Summary
The world around you is filled with mathematical shapes. You just need to start looking for them and you’ll be surprised there are how many of them. It’s like they were always with you as invisible friends. And we have so much to learn from them.
tl;dr
Mathematical shapes and their associated mathematics are everywhere. They can help you foster curiosity in learning.
Nishant Krishna
Latest posts by Nishant Krishna (see all)
- The Psychology behind forming Lifelong Habits - 13 March 2020
- NumberNagar® Dialogue Series – On Making Mathematics the Way of Your Life - 7 February 2020
- NumberNagar® Dialogue Series – On Getting Command in Mathematics - 24 January 2020
- NumberNagar® Dialogue Series – On Bringing Fluency in Spoken English in Children - 17 January 2020
- NumberNagar Dialogue Series – On Creativity in Children - 10 January 2020

