“Given a round tea-cake of some 5 inches across, and two persons of moderate appetite to eat it, in what way should it be cut so as to leave a minimum of exposed surface to become dry?”
Coming across this problem just prior to Christmas in 1906, eminent statistician and polymath of his times, Sir Francis Galton set about solving it. Once he found a satisfactory solution, he sent it out for publication in the journal Nature. The solution was published in the ‘Letters to the Editor’ section of Nature, in December 1906 (Fig. 1)

Fig. 1 – Cutting a Round Cake on Scientific Principles
This short 200-word article is a great lesson about finding Mathematics around us and articulating a scientific concept in a concise and precise manner. For the visually inclined, in this video by Numberphile Alex Bellos, author of Alex’s adventures in Numberland and other popular science books, shows a live demonstration of the solution described in the paper.
On examining the article carefully, two things stand out distinctly.
One – this is not a universal answer to a generic question, what is the best way to cut a cake?
Two – the problem is embedded in a social context and the Mathematics is derived out of it
Let us examine these two points in greater detail.
Specificity:
Stating a problem specifically with as much detail as possible, gives the problem-solving process greater clarity. An illustration is shown below.
- What is the best way to cut a cake?
- What is the best way to cut a round cake?
- What is the best way to cut a round cake of 5 inches diameter?
- What is the best way to cut a round cake of 5 inches diameter, given that 2 persons are going to eat it?
- What is the best way to cut a round cake of 5 inches diameter, given that 2 persons are going to eat it over a period of 3 days?
- What is the best way to cut a round cake of 5 inches diameter in such a way that a minimum amount of exposed surface gets dry, given that 2 persons are going to eat it over a period of 3 days?
By adding one specific detail in each step, we go from a generic question to a highly specific question in a series of six steps. This clarity in articulating the problem makes solving it simpler. Also, the solution is defined specifically for the stated circumstances and nothing more or less.
Students of Maths often fumble in this aspect. Either they are unable to define the given problem with clarity or they do not pay attention to the details in an already well articulated problem. Also, they are impatient to jump into the solving process without clearly understanding what they are expected to solve. Focussing on and addressing this aspect can help many students get over their problem-solving difficulties. At NumberNagar®, we address this aspect by introducing students to the highly effective DPIC (Describe-Plan-Implement-Check) technique of problem solving.
Mathematics is everywhere:
Mathematics is everywhere, only we need the eyes to look for it. This cake cutting problem could have remained a social problem. What Sir Galton perceived was a Mathematical possibility in a seemingly unrelated context. So also, it happens in our everyday lives. All our experiences present us opportunities to perceive Maths and Science in them, if only our minds are inclined in that direction. While academic professionals train themselves to observe Maths and Science in their everyday lives, this is a talent that can be nurtured in young students.
Look at this interesting problem (Fig. 2) – identified and explained by Dr. Prithwijit De in an article titled “A Sweet Seller’s Trick” in the Maths magazine “At Right Angles”, published by the Azim Premji Foundation. The problem here is, “given identical cylindrical bowls, if one sweet seller sells 2 jamuns per bowl and another 3 jamuns per bowl, which one will more customers prefer and therefore, which seller makes more money?”. The geometry of shapes, the calculation of unit costs and profits are all explored with enthusiasm in this “sweet problem”.
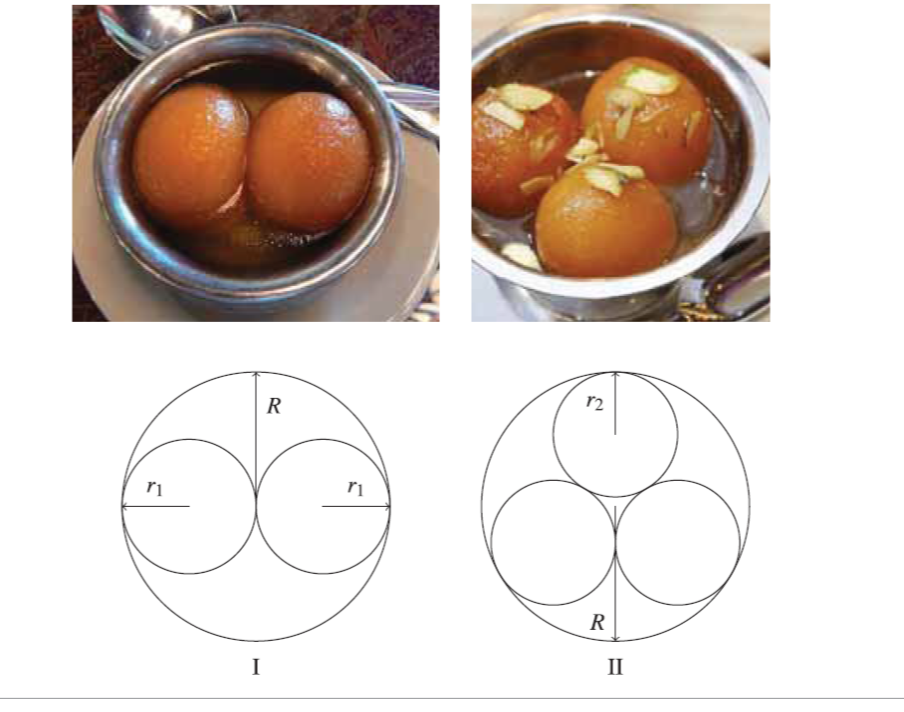
Fig. 2 – Gulab Jamun comparison
Children are innately curious; when directed and nurtured, this curiosity can lead them to find interesting questions and problems in everything they observe around them. Unfortunately, adults have a tendency to curb children’s curiosity, generally due to their inability to answer these questions or frustration with the sheer number of questions that children ask incessantly. Instead if they are encouraged to ask questions and explore to find answers on their own, the excitement of learning is ignited in their minds. And from that excitement, there is no looking back.
The words that struck me the most from Sir Galton’s article were ‘amusement’ and ‘satisfaction’. How often do we start scientific explorations for our own amusement and satisfaction? How often do we encourage our children and young learners to amuse themselves in the learning process? If only we did more of this, learning would be so much more fun.
Let us find it in our hearts to indulge in the process of learning with amusement for personal satisfaction and encourage others to do the same. Maybe then, learning will stop being a chore and reveal its beauty.
Dr. Soumya Sreehari
Latest posts by Dr. Soumya Sreehari (see all)
- To drink water or not to drink – that is the question - 11 June 2021
- Puzzles for fun and learning - 28 May 2021
- A questioning mind is a thinking mind - 14 May 2021
- Play and learn having fun with words - 7 May 2021
- 4 lessons to learn from the Montessori method - 30 April 2021

